EM算法在很多地方都用使用到,比如简单的K-means算法,还有在隐马尔可夫里面,也涉及到了EM算法,可见EM算法在机器学习领域的重要地位。在这里就写一下我对于EM算法的一些理解笔记。后续有新的理解也会追加的。 EM算法的全称叫做:期望最大。EM算法的想法很简单,就像一个人有两条腿向前走,你总是需要固定一条腿动另一条腿这样交替往前走。这里面的两条腿,一个是隐变量,一个是参数θ。 在了解EM算法之前,首先需要了解一些基本的概念。
凹凸函数
这个是《最优化》里面的概念,如果它的二阶导大于0,那么就是凸函数;如果是二阶导小于0,那么就是凹函数。(我记得《最优化》数学老师说,高数的定义和最优化的定义是反着的,因为用的概念不一样,高数好像用的是前苏联的定义,最优化是用的欧洲定义。我也不知道是不是真的……)。这样可能不是很容易记住,所以就取两个很有代表性的函数,方便记忆:凸函数:x2,凹函数:−x2。这样,就是你忘记了定义,也很容易通过这两个函数想越来。更重要的是为了方便你理解下面的概念。
Jensen不等式
这个是EM里面,我认为最重要的一个概念,因为它其实是贯穿整个EM的算法里面的。Jensen不等式的概念也很简单,就是如果是凸函数:f(E(x)) < E(f(x));凹函数:f(E(x)) > E(f(x))。这个定义可能一开始没看明白是什么意思,主要问题可能是那个E(x)的期望。换一个简单的说法, 就是如果是凸函数f(x+y2)<f(x)+f(y)2。这里其实是就是把期望这个公式简化成每个变量出现的概率是1/2,然后你把这个画到f(x)=x2里面就一目了然了。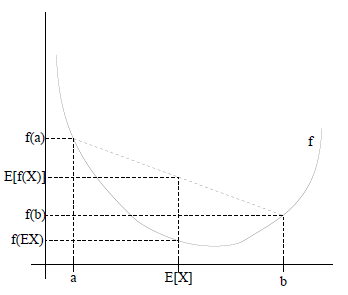
EM算法
给定的训练样本是x(1),...,x(m),我们希望求出最大的概率p(x;θ)。 我们可以求出这个模型的最大似然估计:
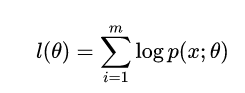
然后取对数:
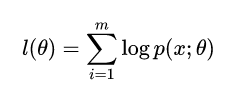
但是,在这个模型里面我们认为p(x;θ)是存在隐变量z的,于是上式改写成
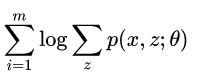
之前求最大似然是很容易,取完对数求导就可以了,但是现在不行,因为有一个隐变量了。那么应该怎么做呢,我们可以固定一个参数,先求另一个参数的最大化,然后再求之前固定的参数。 但是先固定哪个呢,还是随便固定?(这个问题在K-means里面也有,后面再解释。) 这里,我们先观察上面那个式子,直接想出θ是不可能了,因为有z。所以如果想求θ,就一定要固定z。那怎么固定z呢?EM算法就用到了Jensen不等式来估计这个这个z。log是一个凹函数,所以上面那个式子根据不等式是存在一个下界的,那么我们就可以通过下界等式成立的情况来求出最大的z对不对?所以我们可以写出
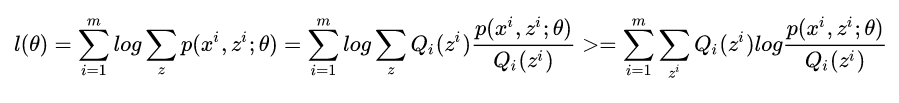
我们可以把jensen的f(x)换log就是上面那个式子了。 EM算法可以写成: 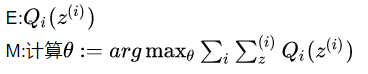
EM推导
EM要解决两个问题,一个是什么时候等式相等;二是为什么一定收敛。
什么时候等式成立呢?
x=E(x)的时候,你带入就会发现两边等式是相等的。因为都是取那一个点,而且概率也一样,所以自然相等。所以就是p(xi,zi;θ)Qi(z(i))=c 然后把Q乘过去,并对所有的z求和,得到:
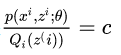
又因为∑zQi(zi)等于1所以∑zp(xi,zi;θ)=c 因此我们可以知道
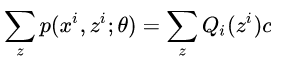
从而EM算法两步可以理解为: 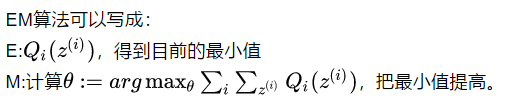
为什么一定收敛?
其实为什么收敛需要解决的一个问题是,是否是单调,如果是单调的话,就可以通过变化幅度来决定。

之所以l(t)<=l(t+1)是因为在M步的时候,θ让公式变大了。所以既然单调,就可以通过变化来证明收敛。 其实这两个问题,也是E与M分别需要解决的问题,E就是让等式成立,而M就是让新状态大于旧状态。